- 全部分类/
- 教育教学/
- 数理天地(高中版)
 扫码免费借阅
扫码免费借阅
目录
快速导航-
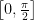
基础精讲 | 导数在破解三角函数问题中的思路分析
基础精讲 | 导数在破解三角函数问题中的思路分析
-
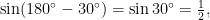
基础精讲 | 转化思想在高中数学解题中的应用研究
基础精讲 | 转化思想在高中数学解题中的应用研究
-
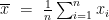
基础精讲 | 分层抽样中的均值与方差问题探究
基础精讲 | 分层抽样中的均值与方差问题探究
-
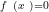
基础精讲 | 高中数学函数零点问题的题型分类及解题思路分析
基础精讲 | 高中数学函数零点问题的题型分类及解题思路分析
-
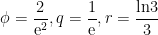
基础精讲 | 函数单调性在实际问题中的应用研究
基础精讲 | 函数单调性在实际问题中的应用研究
-
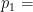
基础精讲 | 概率与统计概念的变式应用及案例解析
基础精讲 | 概率与统计概念的变式应用及案例解析
-
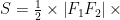
基础精讲 | 中职数学椭圆中焦点三角形的面积求法
基础精讲 | 中职数学椭圆中焦点三角形的面积求法
-
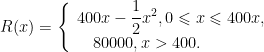
基础精讲 | 基于数学模型的高中数学实际问题解决策略
基础精讲 | 基于数学模型的高中数学实际问题解决策略
-
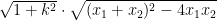
基础精讲 | 中职数学直线与双曲线相交中的弦长问题探究
基础精讲 | 中职数学直线与双曲线相交中的弦长问题探究
-
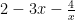
基础精讲 | 基于思维进阶的高中数学习题教学研究
基础精讲 | 基于思维进阶的高中数学习题教学研究
-
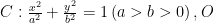
基础精讲 | 走进位置关系,探索转化构建
基础精讲 | 走进位置关系,探索转化构建
-
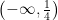
基础精讲 | 高阶思维视角下的高中数学习题教学研究
基础精讲 | 高阶思维视角下的高中数学习题教学研究
-
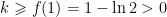
例题精讲 | 神奇的 0
例题精讲 | 神奇的 0
-
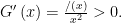
例题精讲 | “凹”"凸”新定义,函数创思维
例题精讲 | “凹”"凸”新定义,函数创思维
-
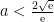
例题精讲 | 巧用“同构”,秒解“指”“对”函数
例题精讲 | 巧用“同构”,秒解“指”“对”函数
-
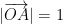
例题精讲 | 向量问题多角度多维度的探索
例题精讲 | 向量问题多角度多维度的探索
-
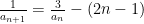
例题精讲 | 深度学习视角下的高中数学“一题多解"研究
例题精讲 | 深度学习视角下的高中数学“一题多解"研究
-
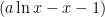
例题精讲 | 变量“双”转“单”,换元法妙用
例题精讲 | 变量“双”转“单”,换元法妙用
-
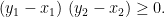
例题精讲 | 高中数学多项选择题分类研究之新概念判定型
例题精讲 | 高中数学多项选择题分类研究之新概念判定型
-

例题精讲 | 由一道高三数学模拟题引发的思维风暴
例题精讲 | 由一道高三数学模拟题引发的思维风暴
-
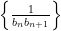
例题精讲 | 例谈数列求和问题的几种常见解法
例题精讲 | 例谈数列求和问题的几种常见解法
-
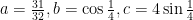
例题精讲 | 化归转化巧拓展,探本溯源妙解答
例题精讲 | 化归转化巧拓展,探本溯源妙解答
-
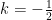
例题精讲 | 高中数学“抛物线及其标准方程”相关习题的解题分析
例题精讲 | 高中数学“抛物线及其标准方程”相关习题的解题分析
-
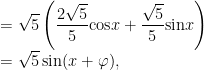
例题精讲 | 三角函数最值问题的分类例析
例题精讲 | 三角函数最值问题的分类例析
-
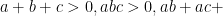
解题技巧 | 高中数学中不等式试题的解题方法探讨
解题技巧 | 高中数学中不等式试题的解题方法探讨
-
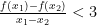
解题技巧 | 巧用函数单调性,妙解高中数学题
解题技巧 | 巧用函数单调性,妙解高中数学题
-
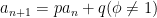
解题技巧 | 借助“四度六步”教学法,妙解高中数学数列难题
解题技巧 | 借助“四度六步”教学法,妙解高中数学数列难题
-
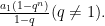
解题技巧 | 高中数学数列求和问题的解题技巧与教学策略研究
解题技巧 | 高中数学数列求和问题的解题技巧与教学策略研究
-
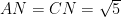
解题技巧 | 高中数学立体几何问题的解题技巧
解题技巧 | 高中数学立体几何问题的解题技巧
-
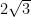
解题技巧 | 梳理思路,智解难题
解题技巧 | 梳理思路,智解难题
-
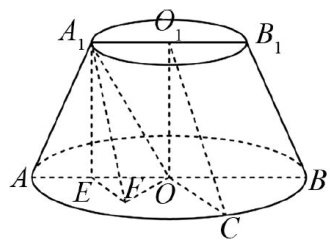
解题技巧 | 点到平面距离问题的解法探究
解题技巧 | 点到平面距离问题的解法探究
-
解题技巧 | 立体几何中平行与垂直问题的解题策略
解题技巧 | 立体几何中平行与垂直问题的解题策略
-
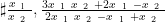
解题技巧 | 圆锥曲线中“非对称问题”的解题策略
解题技巧 | 圆锥曲线中“非对称问题”的解题策略
-

解题技巧 | 跨学科视角下高中数学典型解题案例深度剖析
解题技巧 | 跨学科视角下高中数学典型解题案例深度剖析
-
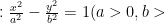
解题技巧 | 基于跨学科思维的高中数学解题教学模式构建
解题技巧 | 基于跨学科思维的高中数学解题教学模式构建
-
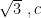
解题技巧 | 数学思想在高中数学解题训练中的妙用
解题技巧 | 数学思想在高中数学解题训练中的妙用
-
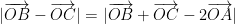
高考高分之路 | 高考中平面向量的几种常见应用分类例析
高考高分之路 | 高考中平面向量的几种常见应用分类例析
-
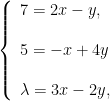
高考高分之路 | 巧用方程铺路通达题解坦途
高考高分之路 | 巧用方程铺路通达题解坦途
-
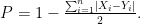
高考高分之路 | 基于SEC模式对新课标I卷与课程标准一致性分析
高考高分之路 | 基于SEC模式对新课标I卷与课程标准一致性分析
-
优化课堂方法 | 基于问题驱动的高中数学概念教学策略探究
优化课堂方法 | 基于问题驱动的高中数学概念教学策略探究
-
优化课堂方法 | 基于大单元的高中数学多元合作学习模式构建方法研究
优化课堂方法 | 基于大单元的高中数学多元合作学习模式构建方法研究
-
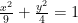
优化课堂方法 | 基于思维导图应用的高中数学高效课堂构建思考
优化课堂方法 | 基于思维导图应用的高中数学高效课堂构建思考
-

优化课堂方法 | 新课标背景下提升高中数学课堂教学效率的措施探讨
优化课堂方法 | 新课标背景下提升高中数学课堂教学效率的措施探讨
-
优化课堂方法 | 探索多媒体技术与高中数学大单元教学的深度融合实践
优化课堂方法 | 探索多媒体技术与高中数学大单元教学的深度融合实践
-
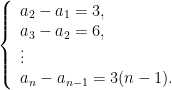
教学思想实践 | 变式教学在高中数学复习课中的实践探索
教学思想实践 | 变式教学在高中数学复习课中的实践探索
-
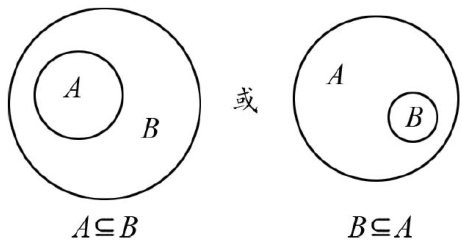
教学思想实践 | 新课改背景下数学思想在高中解题中的渗透策略
教学思想实践 | 新课改背景下数学思想在高中解题中的渗透策略
-
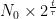
教学思想实践 | 基于数学建模的高中数学问题解决能力培养研究
教学思想实践 | 基于数学建模的高中数学问题解决能力培养研究
-
教学思想实践 | 深度学习视角下高中数学教学的优化策略探究
教学思想实践 | 深度学习视角下高中数学教学的优化策略探究
-
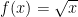
教学思想实践 | 高中数学教学中分层教学模式的实施与效果分析
教学思想实践 | 高中数学教学中分层教学模式的实施与效果分析
-
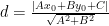
教学思想实践 | 高中解析几何教学中的数形结合思想应用研究
教学思想实践 | 高中解析几何教学中的数形结合思想应用研究
-
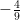
教学经验交流 | 指向思维能力培养的“教材习题”优化开发的实践探讨
教学经验交流 | 指向思维能力培养的“教材习题”优化开发的实践探讨
-
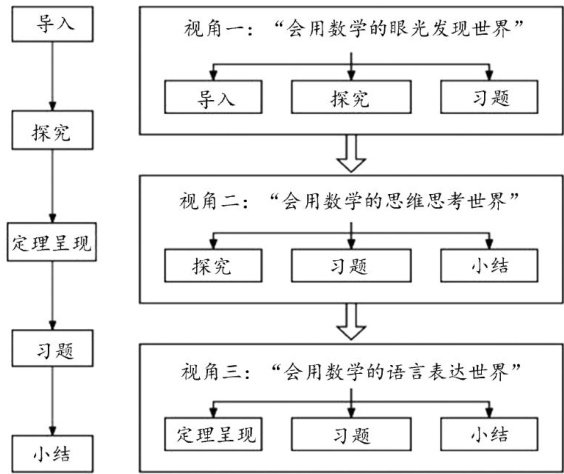
教学经验交流 | “三会"视域下的普高和中职数学教材比较与思考
教学经验交流 | “三会"视域下的普高和中职数学教材比较与思考
-

教学经验交流 | 数学文化融入高中数学课堂教学的实践路径
教学经验交流 | 数学文化融入高中数学课堂教学的实践路径
-
教学经验交流 | 在中职数学教学中融入数学文化的论述
教学经验交流 | 在中职数学教学中融入数学文化的论述
-
教学经验交流 | 新课标下提升高中数学教学有效性的策略
教学经验交流 | 新课标下提升高中数学教学有效性的策略
-
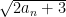
教学经验交流 | 高中数学中数列递推关系的深度剖析与巧妙运用
教学经验交流 | 高中数学中数列递推关系的深度剖析与巧妙运用
-
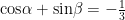
核心素养培养 | 基于数学核心素养的高中数学公式教学策略研究
核心素养培养 | 基于数学核心素养的高中数学公式教学策略研究
-
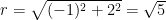
核心素养培养 | 数学抽象核心素养的落实与评价探究
核心素养培养 | 数学抽象核心素养的落实与评价探究
-
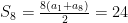
核心素养培养 | 高中数学解题教学中学生高阶思维能力的培养研究
核心素养培养 | 高中数学解题教学中学生高阶思维能力的培养研究
-

核心素养培养 | 核心素养导向下高中数学课堂问题设计与转化案例研究
核心素养培养 | 核心素养导向下高中数学课堂问题设计与转化案例研究
-
核心素养培养 | 高中数学核心素养在日常教学中的落实策略
核心素养培养 | 高中数学核心素养在日常教学中的落实策略
-
核心素养培养 | 核心素养导向下高中数学单元整体教学创新设计策略
核心素养培养 | 核心素养导向下高中数学单元整体教学创新设计策略
-
学生培养研究 | 高中数学三角函数教学中培养学生数学思维能力的策略
学生培养研究 | 高中数学三角函数教学中培养学生数学思维能力的策略
-
学生培养研究 | 例谈高中生数学思维能力的培养措施
学生培养研究 | 例谈高中生数学思维能力的培养措施
-
学生培养研究 | 中职学生三角函数学习兴趣的调查分析与教学应对
学生培养研究 | 中职学生三角函数学习兴趣的调查分析与教学应对
-
学生培养研究 | 高中数学教育中学生自主学习能力的培养路径
学生培养研究 | 高中数学教育中学生自主学习能力的培养路径
-
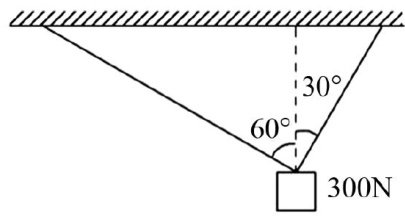
学生培养研究 | 以平面向量为媒介,培养学生的创新思维
学生培养研究 | 以平面向量为媒介,培养学生的创新思维
-
教育技术与数学融合 | 信息技术背景下中职数学的创新教学实施路径研究
教育技术与数学融合 | 信息技术背景下中职数学的创新教学实施路径研究
-
教育技术与数学融合 | 思维可视化在高中数学教学中的应用策略
教育技术与数学融合 | 思维可视化在高中数学教学中的应用策略
-
教育技术与数学融合 | AI智能背景下高中数学智慧课堂教学模式的构建思考
教育技术与数学融合 | AI智能背景下高中数学智慧课堂教学模式的构建思考
-
教育技术与数学融合 | 中职数学教学过程中如何利用DeepSeek辅助教学
教育技术与数学融合 | 中职数学教学过程中如何利用DeepSeek辅助教学
-
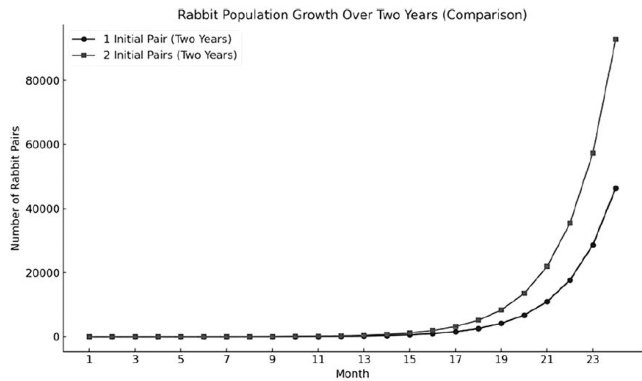
教育技术与数学融合 | 三新背景下AI助力高中数学教学新样态研究
教育技术与数学融合 | 三新背景下AI助力高中数学教学新样态研究
过往期刊
更多-

数理天地(高中版)
2025年23期 -

数理天地(高中版)
2025年22期 -

数理天地(高中版)
2025年21期 -

数理天地(高中版)
2025年20期 -

数理天地(高中版)
2025年19期 -

数理天地(高中版)
2025年18期 -

数理天地(高中版)
2025年17期 -

数理天地(高中版)
2025年16期 -

数理天地(高中版)
2025年15期 -

数理天地(高中版)
2025年14期 -

数理天地(高中版)
2025年13期 -

数理天地(高中版)
2025年12期 -

数理天地(高中版)
2025年11期 -

数理天地(高中版)
2025年10期 -

数理天地(高中版)
2025年09期 -

数理天地(高中版)
2025年08期 -

数理天地(高中版)
2025年07期 -

数理天地(高中版)
2025年06期 -

数理天地(高中版)
2025年05期 -

数理天地(高中版)
2025年04期 -

数理天地(高中版)
2025年03期 -

数理天地(高中版)
2025年02期 -

数理天地(高中版)
2025年01期

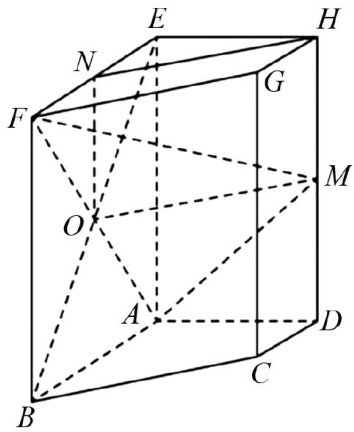
 電或樂 λx1+μx2 等结构的式子,此时 x1,x2 的系数不同,不能直接使用韦达定理,这类问题称为“非对称问题”.本文主要从三个角度给出圆锥曲线中“非对称问题”的解题策略.
電或樂 λx1+μx2 等结构的式子,此时 x1,x2 的系数不同,不能直接使用韦达定理,这类问题称为“非对称问题”.本文主要从三个角度给出圆锥曲线中“非对称问题”的解题策略.








 登录
登录