- 全部分类/
- 教育教学/
- 数理天地(高中版)
 扫码免费借阅
扫码免费借阅
目录
快速导航-

基础精讲 | 神奇的定比点差法及其应用
基础精讲 | 神奇的定比点差法及其应用
-

基础精讲 | 二元表达式最值与范围的深度剖析
基础精讲 | 二元表达式最值与范围的深度剖析
-
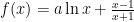
基础精讲 | 依托“导主部分”,解决函数单调性问题
基础精讲 | 依托“导主部分”,解决函数单调性问题
-

基础精讲 | 全概率题型的识别与答题策略
基础精讲 | 全概率题型的识别与答题策略
-

基础精讲 | 向量在高中几何解题中的应用探讨
基础精讲 | 向量在高中几何解题中的应用探讨
-

基础精讲 | 分段函数的常见题型及解题方法
基础精讲 | 分段函数的常见题型及解题方法
-

基础精讲 | 不等式证明的多种方法及其选用策略
基础精讲 | 不等式证明的多种方法及其选用策略
-

基础精讲 | 立体几何中的二面角问题及其解法探究
基础精讲 | 立体几何中的二面角问题及其解法探究
-

基础精讲 | 高中数学解析几何中数形结合思想生成过程探析
基础精讲 | 高中数学解析几何中数形结合思想生成过程探析
-

基础精讲 | 浅谈直线与圆教学中学生易走入的“雷区”
基础精讲 | 浅谈直线与圆教学中学生易走入的“雷区”
-

基础精讲 | 一轮复习“引一讲一练一评一结"教学模式的运用
基础精讲 | 一轮复习“引一讲一练一评一结"教学模式的运用
-

例题精讲 | 巧判定,解“动态”
例题精讲 | 巧判定,解“动态”
-

例题精讲 | 一道直线过定点问题的多解探究
例题精讲 | 一道直线过定点问题的多解探究
-

例题精讲 | 由一道向量题的一题多解引发的思考
例题精讲 | 由一道向量题的一题多解引发的思考
-

例题精讲 | 基于GeoGebra软件的高中数学解题教学研究
例题精讲 | 基于GeoGebra软件的高中数学解题教学研究
-

例题精讲 | 圆锥曲线斜率定值问题的两种解题思路
例题精讲 | 圆锥曲线斜率定值问题的两种解题思路
-

例题精讲 | 关于立体几何翻折问题的教学探究
例题精讲 | 关于立体几何翻折问题的教学探究
-

例题精讲 | 翻折叠,抓“不变”
例题精讲 | 翻折叠,抓“不变”
-

例题精讲 | 例析导数在三类题型中的应用
例题精讲 | 例析导数在三类题型中的应用
-

例题精讲 | 万变不离其宗的“新定义”
例题精讲 | 万变不离其宗的“新定义”
-

例题精讲 | 数形结合思想在函数图象中的实践路径
例题精讲 | 数形结合思想在函数图象中的实践路径
-

例题精讲 | 空间几何体内嵌问题专题复习
例题精讲 | 空间几何体内嵌问题专题复习
-

解题技巧 | 高中数学抛物线常考题型的解题技巧
解题技巧 | 高中数学抛物线常考题型的解题技巧
-

解题技巧 | 应用不同数学思想解答三角函数问题的分析
解题技巧 | 应用不同数学思想解答三角函数问题的分析
-

解题技巧 | 拓展隔板法在高中数学解题中的应用
解题技巧 | 拓展隔板法在高中数学解题中的应用
-

解题技巧 | 用构造函数法解比较大小问题
解题技巧 | 用构造函数法解比较大小问题
-

解题技巧 | 探究换元法在高中数学解题中的应用
解题技巧 | 探究换元法在高中数学解题中的应用
-

解题技巧 | “导数法"在研究含参函数极值、最值问题上的应用
解题技巧 | “导数法"在研究含参函数极值、最值问题上的应用
-

解题技巧 | 探究圆锥曲线最值问题的解题方法
解题技巧 | 探究圆锥曲线最值问题的解题方法
-

解题技巧 | 用均值不等式求函数最值的几种方法探究
解题技巧 | 用均值不等式求函数最值的几种方法探究
-

解题技巧 | 借助导数知识突破高中数学解题困境
解题技巧 | 借助导数知识突破高中数学解题困境
-

高考高分之路 | 新高考数学多选题的特点及解题策略
高考高分之路 | 新高考数学多选题的特点及解题策略
-

高考高分之路 | 探究构造函数法在高考试题中的应用
高考高分之路 | 探究构造函数法在高考试题中的应用
-

高考高分之路 | 高考命题视角下的复数复习策略
高考高分之路 | 高考命题视角下的复数复习策略
-

高考高分之路 | 新高考背景下数列与解析几何的综合形势
高考高分之路 | 新高考背景下数列与解析几何的综合形势
-

高考高分之路 | 高考内容改革下高中数学教学分析
高考高分之路 | 高考内容改革下高中数学教学分析
-
优化课堂方法 | 以问题为驱动的引导式高中数学教学
优化课堂方法 | 以问题为驱动的引导式高中数学教学
-

优化课堂方法 | 高中数学教学中引入探究性学习的策略分析
优化课堂方法 | 高中数学教学中引入探究性学习的策略分析
-

优化课堂方法 | “三新”背景下的高中数学教学策略探究
优化课堂方法 | “三新”背景下的高中数学教学策略探究
-

优化课堂方法 | 高中数学课堂教学的导入方法分析
优化课堂方法 | 高中数学课堂教学的导入方法分析
-

优化课堂方法 | “三新"背景下高中数学大单元教学实施策略研究
优化课堂方法 | “三新"背景下高中数学大单元教学实施策略研究
-

优化课堂方法 | “双新”视角下高中数学一境到底情境创设
优化课堂方法 | “双新”视角下高中数学一境到底情境创设
-

优化课堂方法 | 新课改下高中数学课堂提问有效性策略
优化课堂方法 | 新课改下高中数学课堂提问有效性策略
-
教学思想实践 | 基于深度学习的高中数学单元教学分析
教学思想实践 | 基于深度学习的高中数学单元教学分析
-
教学思想实践 | 基于项目式学习的高中数学课程设计与实践
教学思想实践 | 基于项目式学习的高中数学课程设计与实践
-

教学思想实践 | 基于深度学习的高中数学概念学习现状调查与分析
教学思想实践 | 基于深度学习的高中数学概念学习现状调查与分析
-

教学思想实践 | 基于深度学习的高中数学学科素养提升策略研究
教学思想实践 | 基于深度学习的高中数学学科素养提升策略研究
-

教学思想实践 | 基于SOLO分类理论的高中数学有效提问
教学思想实践 | 基于SOLO分类理论的高中数学有效提问
-
教学思想实践 | 关键能力培养视域下的高中数学项目式教学策略研究
教学思想实践 | 关键能力培养视域下的高中数学项目式教学策略研究
-
教学经验交流 | 立足课堂,育人育心
教学经验交流 | 立足课堂,育人育心
-

教学经验交流 | 探讨分式函数值域求解的多种方法及其理论基础
教学经验交流 | 探讨分式函数值域求解的多种方法及其理论基础
-
教学经验交流 | 高中数学A版教材中集合的基本运算教学策略研究
教学经验交流 | 高中数学A版教材中集合的基本运算教学策略研究
-
教学经验交流 | 新课改形势下高中数学课堂教学提问艺术浅探
教学经验交流 | 新课改形势下高中数学课堂教学提问艺术浅探
-
教学经验交流 | 指向理解的高中数学阅读教学实践研究
教学经验交流 | 指向理解的高中数学阅读教学实践研究
-

教学经验交流 | 课程教学改革深化下初高中数学衔接教学现状调研报告
教学经验交流 | 课程教学改革深化下初高中数学衔接教学现状调研报告
-

核心素养培养 | 高中数学核心素养培育的有效策略探微
核心素养培养 | 高中数学核心素养培育的有效策略探微
-

核心素养培养 | 核心素养背景下高中数学函数大单元教学的实践研究
核心素养培养 | 核心素养背景下高中数学函数大单元教学的实践研究
-
核心素养培养 | 核心素养视野下高中生数学运算能力的提升对策
核心素养培养 | 核心素养视野下高中生数学运算能力的提升对策
-
核心素养培养 | 数学与应用数学教学中培养学生核心素养的策略与实践
核心素养培养 | 数学与应用数学教学中培养学生核心素养的策略与实践
-
核心素养培养 | 高中数学函数大单元教学与核心素养融合的实践探索
核心素养培养 | 高中数学函数大单元教学与核心素养融合的实践探索
-

学生培养研究 | 基于培养说理能力的高中数学教学探究
学生培养研究 | 基于培养说理能力的高中数学教学探究
-

学生培养研究 | 高中数学教学中学生创造性思维能力养成概述
学生培养研究 | 高中数学教学中学生创造性思维能力养成概述
-
学生培养研究 | 数学文化视角下高中数学教学对学生生涯规划的影响
学生培养研究 | 数学文化视角下高中数学教学对学生生涯规划的影响
-
学生培养研究 | 在高中数学教学中培养学生逆向思维能力的策略研究
学生培养研究 | 在高中数学教学中培养学生逆向思维能力的策略研究
-
学生培养研究 | 基于“问题解决”的高中数学逻辑推理能力的培养路径研究
学生培养研究 | 基于“问题解决”的高中数学逻辑推理能力的培养路径研究
-

信息技术与数学融合 | 信息技术如何与数学实验深度融合的教学研究
信息技术与数学融合 | 信息技术如何与数学实验深度融合的教学研究
-
信息技术与数学融合 | 信息技术与高中数学概念教学深度融合
信息技术与数学融合 | 信息技术与高中数学概念教学深度融合
-
信息技术与数学融合 | “智慧课堂”下高中数学核心素养的培养研究
信息技术与数学融合 | “智慧课堂”下高中数学核心素养的培养研究
-
信息技术与数学融合 | 关于“互联网+” 与中职数学教学智慧转型的思考
信息技术与数学融合 | 关于“互联网+” 与中职数学教学智慧转型的思考
-
信息技术与数学融合 | 数字教学背景下高中数学作业设计的思考和探究
信息技术与数学融合 | 数字教学背景下高中数学作业设计的思考和探究
过往期刊
更多-

数理天地(高中版)
2025年23期 -

数理天地(高中版)
2025年22期 -

数理天地(高中版)
2025年21期 -

数理天地(高中版)
2025年20期 -

数理天地(高中版)
2025年19期 -

数理天地(高中版)
2025年18期 -

数理天地(高中版)
2025年17期 -

数理天地(高中版)
2025年16期 -

数理天地(高中版)
2025年15期 -

数理天地(高中版)
2025年14期 -

数理天地(高中版)
2025年13期 -

数理天地(高中版)
2025年12期 -

数理天地(高中版)
2025年11期 -

数理天地(高中版)
2025年10期 -

数理天地(高中版)
2025年09期 -

数理天地(高中版)
2025年08期 -

数理天地(高中版)
2025年07期 -

数理天地(高中版)
2025年06期 -

数理天地(高中版)
2025年05期 -

数理天地(高中版)
2025年04期 -

数理天地(高中版)
2025年03期 -

数理天地(高中版)
2025年02期 -

数理天地(高中版)
2025年01期










 登录
登录