全部分类/
教育教学/
高中数理化

高中数理化

2025年03期

北师大集团核心刊物

扫码免费借阅

目录

快速导航

名师工作室 | 复数中五类创新题型分类赏析

名师工作室 | 复数中五类创新题型分类赏析

复数是高考的必考考点，考查方向主要体现在以下几个方面：一是了解引入复数的必要性，理解复数的相关概念（定义、模、实部与虚部、共轭复数等）;二是掌握复数的代数表示及其几何意义（复数与复平面上点的对应关系）;三是掌握复数代数形式的加、减、乘、除运算法则，尤其是要熟练掌握复数的除法运算;四是关注复数的新颖性和交会性．下面从全国各地模拟卷中精选五类创新题型并结合典型例题予以深刻剖析，旨在探索题型规律，揭示解
高考全关注 | 勇破思维“卡点”决胜新高考

高考全关注 | 勇破思维“卡点”决胜新高考

2023年高考数学全国甲卷理科第18题是一道反套路、反机械刷题的典型试题，题目本身并不难，但是与考生平时训练的题不太一样，结合直线CA１，CA ，CB互相垂直这一条件，考生极易考虑用坐标法解题．但随着解题过程的深入，解题难度逐渐增大，导致有些考生无法顺利完成解题或选择直接放弃．是什么原因导致这种情况的发生？说到底就是数学功底不扎实，或者说功底还可以，但就是缺少勇毅前行和数学理性探索的精神．
高考全关注 | 新高考数学中无棱二面角问题的常见处理策略

高考全关注 | 新高考数学中无棱二面角问题的常见处理策略

立体几何是高中数学教材中的重要内容，也是新高考必考的内容．在近几年的新高考数学试题中，有一类无棱二面角问题：只在图形中给出了二面角的两个半平面的一个公共点，没有给出二面角的棱．这类问题的求解令广大考生无从下手．基于此，本文以近几年的高考题及模拟题为例，说明无棱二面角问题的常见处理策略，供读者参考．
聚焦新课程 | 回归教材　精准备考

聚焦新课程 | 回归教材　精准备考

高考数学向来坚持源于教材、高于教材的命题思想，回归教材是永不褪色的主题．2024年的高考试题更是把回归教材体现得淋漓尽致．那么回归教材具体可以做什么？笔者以2024年新课标Ⅰ卷第17题为例，深入研究学习，感触颇多.
聚焦新课程 | 从不疑处找疑

聚焦新课程 | 从不疑处找疑

2024年浙江省高考数学因首次采用新课标Ⅰ卷而备受师生关注．高考作为教学的指挥棒，决定了教师怎样教，学生怎样学．作为高中数学教师，笔者始终关注高考动态，长期研究高考试题类型和来源，经过多年的分析、类比、反思和探索，总结出几大特征，对学生平时的学习和备考提出如下建议．
强基竞赛 | 强基计划中有关圆锥曲线的基本问题

强基竞赛 | 强基计划中有关圆锥曲线的基本问题

１知识补充
题根研究 | 圆锥曲线不联立之定比点差法

题根研究 | 圆锥曲线不联立之定比点差法

北宋诗人苏轼在«题西林壁»中有这样两句诗：横看成岭侧成峰，远近高低各不同．这启示我们，站在不同的角度看待同一个事物，往往能够见到不同的“风景”，帮助我们更加全面而深刻地认识问题，从而更好地解决问题．高中数学解析几何中的圆锥曲线问题，往往因烦琐、复杂的运算过程，成为学生高考的“拦路虎”．为此，本文基于平面向量的运算，从坐标的角度看待圆锥曲线问题，给出利用定比点差法解决圆锥曲线问题的解题策略．
题根研究 | 聚焦核心素养　探究优化解法

题根研究 | 聚焦核心素养　探究优化解法

解析几何是高考数学中的重难点，是提升学生数学抽象、逻辑推理、数学运算等能力的重要素材．笔者以一道解析几何问题为例，从试题剖析、解法探究以及解法总结等方面对解析几何备考进行分析和探究，解密几何问题代数化的多种方法，希望能够为读者起到抛砖引玉的作用．
题根研究 | 由一道高考题的错误解法谈椭圆参数方程的应用

题根研究 | 由一道高考题的错误解法谈椭圆参数方程的应用

在一堂直线与圆锥曲线的交点高考复习课中，笔者给出了2020年浙江卷第21题．学生写出若干种不同的解法，其中一种是椭圆的参数方程的解法，但是所得答案却是错误的，学生心存疑虑，不得其解．笔者给予了引导，进行错误分析，并总结利用椭圆的参数方程解题的特点，以期帮助他们提升解决同类问题的能力．
题根研究 | 如何求平面向量的模

题根研究 | 如何求平面向量的模

向量是近代数学中重要的基本概念．向量既有几何形式（有向线段）又有代数形式（坐标法表示），既有大小（长度）又有方向（夹角），所以与向量有关的数学问题具有很强的灵活性．向量是连接数学各分支（包括平面几何、解析几何、立体几何、三角函数和不等式等）的桥梁和纽带，给传统数学注入了新的活力和无限生机．平面向量是新高考必考内容，尤其是求平面向量的模，是高考选择题与填空题中的常见题型．那么如何求平面向量的模呢？
题根研究 | 一道曼哈顿距离问题的探究及思考

题根研究 | 一道曼哈顿距离问题的探究及思考

现行教材中出现了度量平面上两点远近的几种距离
考题分类评析 | “隐圆”助力显奇效,直观想象提素养

考题分类评析 | “隐圆”助力显奇效,直观想象提素养

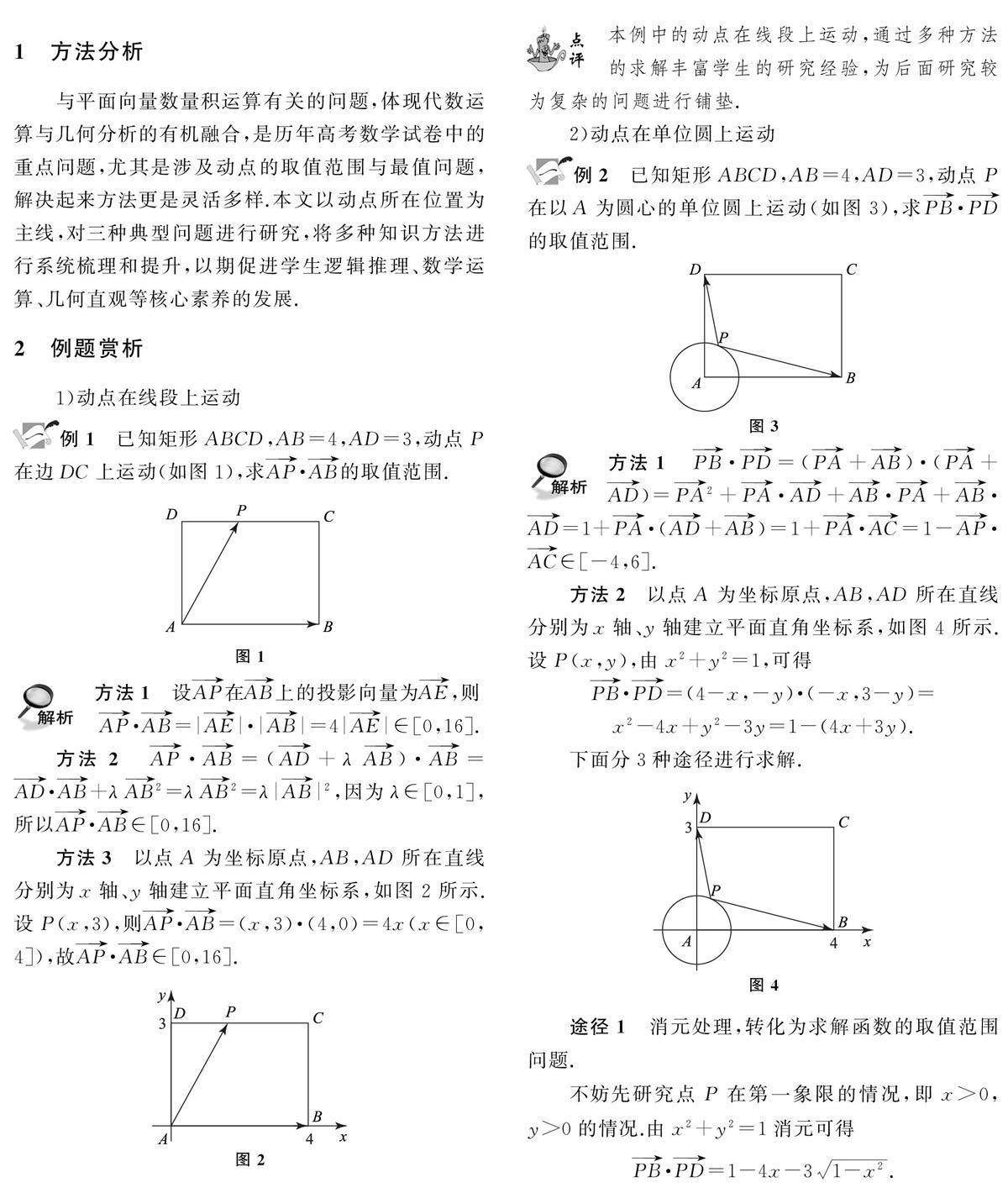
直观想象是高中数学的六大核心素养之一，其关键是通过对题目信息进行有效转化与联想，合理构造几何图形，借助图形分析数学问题，建立形与数的联系，将复杂的问题简明化，探索解决问题的思路，并最终解决问题．通过对平面向量考题的分析发现，部分考题的背景呈现出一个显著特点就是与圆有关，下面总结常见“隐圆”的模型与特征，并结合具体例题归纳此类问题的一般解题途径与策略．
考题分类评析 | 平面向量数量积中有关动点问题的研究

考题分类评析 | 平面向量数量积中有关动点问题的研究

１方法分析
考题分类评析 | 正方体背景下立体几何问题的思维方式

考题分类评析 | 正方体背景下立体几何问题的思维方式

以正方体为背景的立体几何综合题，在近几年高考中经常以多选题的形式出现．这类问题综合性强、涉及的知识广、求解思维方式灵活，能有效考查学生的空间想象能力、化归与转化能力．学生解题时漏选、错选的情况时有发生．基于此，本文提出解答此类问题的思维方式，供读者参考．
考题分类评析 | 反模型视域下的外接球问题

考题分类评析 | 反模型视域下的外接球问题

空间几何体外接球问题是立体几何的难点之一，很多教辅资料上都介绍解答外接球问题的各种模型，如墙角模型、汉堡模型、对棱相等模型、斗笠模型等．然而，这些模型却很难直接用于近两年的高考真题，其根本原因是以检测核心素养与关键能力为目标的考试是反模型化的，而且这种反模型化趋势可能会成为常态．因此，学生有必要掌握好通性通法，以不变应万变．
重点辅导 | 直击两曲线的公切线问题

重点辅导 | 直击两曲线的公切线问题

两曲线的公切线问题是高考的热点题型，其中单一曲线的切线问题相对简单，但两曲线的公切线问题相对复杂，解题的关键是对公切线这一条件进行转化．那么两曲线的公切线问题主要有哪些题型，每一种题型又该如何破解？本文举例说明．
重点辅导 | 圆锥曲线综合题解答感悟

重点辅导 | 圆锥曲线综合题解答感悟

圆锥曲线综合题在高考命题中常以把关题的形式出现，题目思维量大、计算烦琐，能有效考查学生化归转化、推理论证、运算求解等能力，因此备受命题人的关注．本文以一道椭圆综合题为例，谈几点解题感悟，希望对读者有所帮助．
重点辅导 | 椭圆与双曲线焦点三角形的美丽性质

重点辅导 | 椭圆与双曲线焦点三角形的美丽性质

本文的定理１、定理２与例５给出了椭圆与双曲线的焦点三角形的美丽性质，并介绍了其应用．
重点辅导 | 建系处理,巧解向量题

重点辅导 | 建系处理,巧解向量题

众所周知，平面向量具有“数”和“形”的双重性质．那么，在具体解题时，如何巧妙利用该双重性质呢？一般地，处理与平面图形有关的平面向量问题时，若能灵活建立平面直角坐标系，则可借助向量的坐标运算解题，这体现了向量代数化的重要性．
重点辅导 | “补体法”在立体几何解题中的妙用

重点辅导 | “补体法”在立体几何解题中的妙用

解决立体几何相关问题，有时需要将某些几何体补成熟悉的几何体（如正方体、长方体和圆柱体等），这就是所谓的“补体法”．这种方法能帮助学生充分利用“补体”后得到的新几何体的特征，从整体上把握问题实质，从而快速找到解题思路．那么，“补体法”在立体几何问题中有哪些妙用呢？本文举例说明．
难点挑战 | 向量等和线与等和面的应用

难点挑战 | 向量等和线与等和面的应用

在人教版、苏教版等教材以及历年高考真题中，经常出现以向量等和线为背景的题目，因此该理论及其应用成为热点．关于等和线的文章有很多，但其内容大多局限于求平面向量系数线性关系式的值或取值范围这一问题上．鉴于此，本文一方面将平面向量等和线理论拓展到空间向量等和面理论;另一方面，通过举例说明的方式拓展其应用，并推导出诸多有趣的结论，以期提高学生的数学学科核心素养和解决问题的能力．
难点挑战 | 圆锥曲线的一种统一方程及其应用

难点挑战 | 圆锥曲线的一种统一方程及其应用

１圆锥曲线统一的直角坐标方程
难点挑战 | 巧构向量妙解题

难点挑战 | 巧构向量妙解题

向量有着数与形的双重特征，它将代数与几何紧密相连．对于某些数学问题，通过构造向量可以实现问题之间的转化，将复杂问题变得简单，将陌生问题变得熟悉．构造向量解题体现了化归与转化的数学思想，对解题者数学素养的提升大有益处．
方法与技巧 | 在解三角形中倍长定分线问题的求解对策

方法与技巧 | 在解三角形中倍长定分线问题的求解对策

解三角形问题是高考中常见的题型，根据所给条件的不同，问题的形式也有所不同，其中题目中给出某点在三角形的一边上，且将该线段按照一定比例分割，这类问题被称为倍长定分线问题．此类问题的解决有其特殊性，本文在研究典型例题的基础上，归纳出四种常用的方法．
方法与技巧 | 运用向量求解几何问题

方法与技巧 | 运用向量求解几何问题

在高中数学中，向量拥有一整套的理论知识与方法，它是沟通代数与几何的“局域网”．遇到几何问题时，如果能用向量的观点去分析，往往会收获意想不到的效果．尤其是对于有些几何问题，用常规的方法处理可能较为烦琐，甚至无效，此时不妨考虑用向量法求解．本文举一些例子加以说明，以期给读者带来启发和帮助．
方法与技巧 | 求解向量数量积问题的四种途径

方法与技巧 | 求解向量数量积问题的四种途径

向量数量积的运算是平面向量内容的主要考点，考查题型有求值、求最值和求取值范围等．求解此类问题的关键是选择恰当的基底分解向量，那么常见的分解途径有哪些呢？
方法与技巧 | 圆锥曲线中点弦问题的常见题型及求解策略

方法与技巧 | 圆锥曲线中点弦问题的常见题型及求解策略

圆锥曲线与直线相交的中点弦问题是解析几何综合题中的典型问题．此类问题的求解是有章可循的，其中点差法就是一种高效的解题方法．由于中点弦问题有多种表现形式，不同问题的解题方法也各有区别，因此本文举例介绍常见的几种题型，并揭示其特定的求解策略，供读者参考．
方法与技巧 | 圆锥曲线中的动点在定直线上的问题求解方法

方法与技巧 | 圆锥曲线中的动点在定直线上的问题求解方法

求证动点在某条定直线上是常考的一类题型．这类问题主要考查数学运算和逻辑推理素养，无论从思维角度还是运算角度看，都具有一定难度．那么这类问题该如何解呢？本文举例说明．

过往期刊

更多

猜你喜欢

衢州职业技术学院电子阅览室